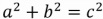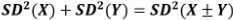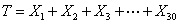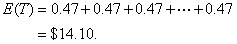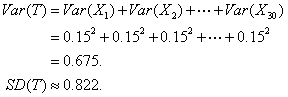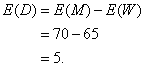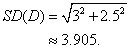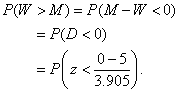Pythagorean Theorem of Statistics
Overview:
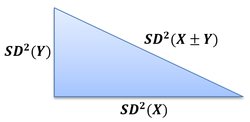
This theorem states that, for independent random samples, the square of the standard deviation is their sum is the sum of the squares of their standard deviations.
Conditions:
Each trial must be independent.
Equations:
The equation for the usual Pythagorean Theorem is:
This theorem states that, for independent random samples, the square of the standard deviation is their sum is the sum of the squares of their standard deviations.
Conditions:
Each trial must be independent.
Equations:
The equation for the usual Pythagorean Theorem is:
The equation for the new “Pythagorean Theorem of Statistics” is
Variances:
It is easier to write the Pythagorean Theorem of Statistics using variances: Var(X±Y)=Var(X)+Var(Y). When you are looking for the sum OR difference of two variables, you always ADD the variances.
Example 1:
At Matt and Dave's, every Thursday was Roll-the-Dice Day, allowing patrons to rent a second video at a discount determined by the digits rolled on two dice. Students were told that these second movies would cost an average of $0.47 with a standard deviation of $0.15. If a customer rolls the dice and rents a second movie every Thursday for 30 consecutive weeks, what is the approximate probability that the total amount paid for these second movies will exceed $15.00?
1. First, we note that the total amount of money paid over thirty days is the sum:
It is easier to write the Pythagorean Theorem of Statistics using variances: Var(X±Y)=Var(X)+Var(Y). When you are looking for the sum OR difference of two variables, you always ADD the variances.
Example 1:
At Matt and Dave's, every Thursday was Roll-the-Dice Day, allowing patrons to rent a second video at a discount determined by the digits rolled on two dice. Students were told that these second movies would cost an average of $0.47 with a standard deviation of $0.15. If a customer rolls the dice and rents a second movie every Thursday for 30 consecutive weeks, what is the approximate probability that the total amount paid for these second movies will exceed $15.00?
1. First, we note that the total amount of money paid over thirty days is the sum:
2. Second, we find the expected total:
3. Third, we apply the Pythagorean theorem of statistics to get the standard deviation:
Remember: to get from variance to standard deviation, you take the square root of the variance. Therefore, the square root of 0.675 is 0.822.
4. Fourth, understand that based on the Pythagorean Theorem of Statistics, With n = 30 here, we can safely estimate the probability that T > 15.00 by working with the model N(14.10, 0.822).
Example 2:
Consider heights of men and women. The heights of each sex are described by a normal model; the means are 70 inches for men and 65 inches for women, with standard deviations of 3 inches and 2.5 inches respectively. Suppose a married man and a married woman are each selected at random. What is the probability the woman will be taller than the man?
1. First, define the random variables: M = Height of the chosen man, W = Height of the woman, D = Difference in their heights: D = M – W.
2. Second, plug in values for D:
4. Fourth, understand that based on the Pythagorean Theorem of Statistics, With n = 30 here, we can safely estimate the probability that T > 15.00 by working with the model N(14.10, 0.822).
Example 2:
Consider heights of men and women. The heights of each sex are described by a normal model; the means are 70 inches for men and 65 inches for women, with standard deviations of 3 inches and 2.5 inches respectively. Suppose a married man and a married woman are each selected at random. What is the probability the woman will be taller than the man?
1. First, define the random variables: M = Height of the chosen man, W = Height of the woman, D = Difference in their heights: D = M – W.
2. Second, plug in values for D:
3. Use the Pythagorean Theorem to find the standard deviation:
4. Use a z-score to find the probability that the woman is taller: